In my earlier post, we saw what a T-Nut is and how we go about cracking a T-Nut.
We started with a step by step approach and soon realized, that the first of those stages is culling the epicarp. We also stated, that sometimes, the culling by itself, can get us to close proximity of the solution.
Let’s take a typical example to illustrate what that means.
The Problem Statement
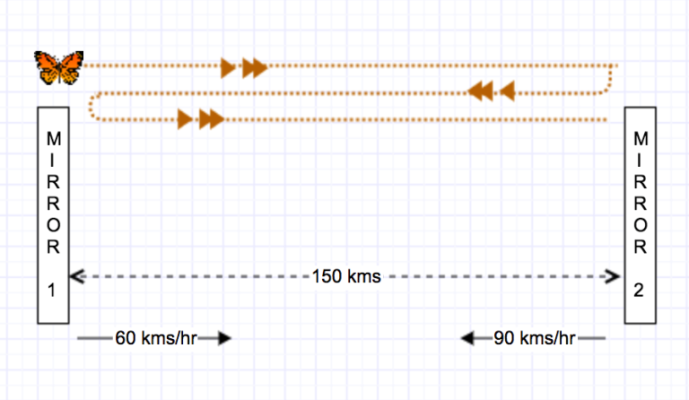
Consider a scenario as below
Two mirrors 150 kms apart are travelling towards each other along a straight line.
The first mirror is travelling at 60 kms per hour,
while the second rushes along at 90 kms per hour.
A butterfly is fluttering on top of the first mirror.
It bustles from one mirror to the other.
On reaching a mirror, it turns around immediately, and scurries back towards the other,
and on reaching it turns around again.
It goes on flying back and forth between the two mirrors until they collide.
The butterfly is moving at a constant speed but much faster than the two mirrors.
For all practical purposes, assume the below
"The butterfly does not lose any time or speed when turning around"
Also assume the change of direction while turning around is spontaneous.
The coefficient of friction (µ) on both mirrors is assumed to be 0,
while the coefficient of reflection on both mirrors is assumed to be 1.
What is the velocity of the butterfly?
The Solution
So how did you feel reading that epic?
Didn’t the question feel complicated? Even though, there was abundance of information.
That’s because of lack of pertinent context connecting the information dots.
With so much that was said, let’s try to extract the relevant info from the eloquent barrage.
If you are not from a physics background and did not understand quite a few terms there, well, not to worry.
The only thing you ever need to know is what it means by “velocity”.
Velocity is defined as total displacement over time.
V = Displacement/time
Displacement is the total distance moved relative to the point where we started. So in a round trip, the displacement is 0, distance however is not.
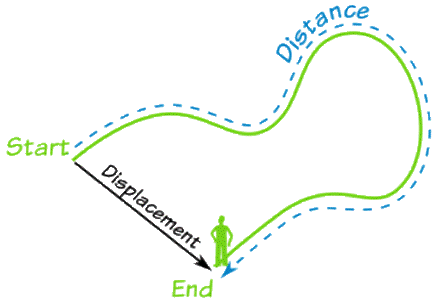
At the end of it all, though the butterfly did move around a lot, from one mirror to another, back and forth, it actually didn’t quite displace much.
Getting that is the crux of the problem.
Everything else you see - the long verbose description, the coefficient of friction and reflections… are all distractions… are all epicarps.
Let’s cull it then.
All you need to do is now find the total distance moved by mirror-1 before colliding with mirror-2.
Because the displacement of the butterfly is how far mirror-1 has moved from the initial point.
Wonder why? The butterfly started at the same point remember?
Ting, Ring - Does that ring a bell?
If that’s understood, this is a simple relative velocity problem.
Time taken to collide is calculated as below
Distance = 150 kms
Relative speed since trains are moving towards each other =
90 + 60 = 150 kms/hr
Total time thus = 150/(90+60) = 1 hr
So distance travelled by mirror-1 in this 1 hour is
1 hr * 60 kms/hr = 60 kms
So total velocity of the butterfly is
60 kms/1 hr = 60 kms/hr
60 kms per hour. Awesome right?
Piece of cake, iff we set aside the epicarp
The Learning
Is it loud and clear now? Do you see how much difference picking the relevant info from a problem statement makes?
We tend to understand the problem so much better, when we focus on the specifics.
Once, we understand the problem, solving it is a breeze.
Just a hammer away !!!
If culling the epicarp doesn’t yet get you to the solution, try out the subsequent steps.