Welcome to another stint of T-Nut.
This time the knot we are trying to untangle is the one pertaining to a singly linked-list.
It all started with a typical Little B conundrum, during tea time.
The formal problem statement would be as below.
Given a singly linked list, reverse its every 'n' nodes
The sample input and respective outputs expected are as below
Input: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> NULL and n = 2
Output: 2 -> 1 -> 4 -> 3 -> 6 -> 5 -> NULL.
Input: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> NULL and n = 3
Output: 3 -> 2 -> 1 -> 6 -> 5 -> 4 -> 8 -> 7 -> NULL.
The Thought Train
Here’s a typical T-Nut, let’s begin cracking it, shall we?
Let’s use the analogy that we just devised, of chewing on an unknown fruit, to crack it.
Here goes.
Step1 - Cull the epicarp
First we need to isolate the problem statement.
But, that’s already done for us. Let’s re-look at what we have.
-
The Naïve Problem Statement
This as I understand is to reverse a linked list with some constraints -
Let me nibble on The Buzz Words now
Singly Linked List
What do I get out of this?
i. Size is unavailable and can be tremendously huge.
ii. An item cannot be accessed based on index/position. I need to get to every item.
iii. The traversal is unidirectional. We cannot move back and forth.
Reverse in blocks of "n"
Well, doesn’t quite sit pretty in the head, but let me move on. I will let it dawn on me.
Step2 - Take the first bite
Let’s next devise a strategy to solve this.
- Visual Representation
Since I can’t think of any similar problem I’ve solved, let me try something closer to real life.
The first realistic thing that comes to my mind when we say linked list, is a train with bogies.
Let me create a 2D train with bogies representing nodes. The values of the nodes represent the solitary passenger, commuting in them

- Analyze input output samples
- Solve it mentally
Let’s see if I understand the input, output samples
Input:
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> NULL, ok a list with 6 elements
And n=2
Reverse the first two elements
2 -> 1
Reverse the next two
4 -> 3
Finally, Reverse the last two
6 -> 5
Putting them together
2 -> 1 -> 4 -> 3 -> 6 -> 5 -> NULL
Alright, feels like now, I can easily guess the output from the input. Time to chew on the bite now.
Step3 - Chew and swallow the bite
Let’s next try to transform our strategy into workable logic.
- Identify edge cases
In the second sample, we have
Input:
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> NULL, ok a list with 8 elements
And n=3
So let me reverse, group of three elements
3 -> 2 -> 1
6 -> 5 -> 4
8 -> 7
Putting them together
3 -> 2 -> 1 -> 6 -> 5 -> 4 -> 8 -> 7 -> NULL
Ok, there is an edge case. If 3 elements are not available, it should reverse whatever is available. That’s a good catch.
Let me try to garnish some logic now
- Create a logical flow
Let me first see how Mr.Pristine went about it
i. He first split the linked list in batches of “n”
ii. He then reversed the sub link list
Let me pen down some workable logic for the same
Splitting a linked list
This should be straight forward, I keep moving across the list and pick “n” nodes
Markers
How do I work on the picked ones?
Should I make a copy of them all, or use the existing nodes?
Let me connect back to my visual representation, to try answering that.
If I choose to copy, I may end up making a copy of the whole train. I mean that’s freaking bulky and not space effective.
(See? Visualizing helps you understand the inefficiencies sometimes)
<Bookmark Alert!>
Keep a bookmark of this please, we’ll get back to this soon
Reversing a linked list
How did Mr.Pristine do that?
Well he went to the last item in each sub-list, and then put the numbers in reverse.
Hey… wait… WTF in that? How can he do that?
I thought, you cannot traverse back in a singly linked list!!
But for Mr Pristine, there is no such thing as a singly linked list. There are no constraints. The cheater just started walking in reverse direction.
As we call out the bluff of Mr.Pristine, let’s emphasize the constraints for him.
Let’s present the problem through our train analogy adding an explicit constraint
Even in train bogies, we can move back and forth, so,
'Assume there is a guard standing at the door preventing you from going back.
He will only let you go forward'
So we have a physical separation through bogies and we’ve also ensured unidirectional movement
Redefined problem statement
With all those analogies, what does reversing now mean?
We need to make sure the passengers in bogies are relocated. And the relocation constraint is reversal in blocks of ‘n’.
Quite clear?
So we’ve redefined the problem, through something that we know very well - A train with bogies.
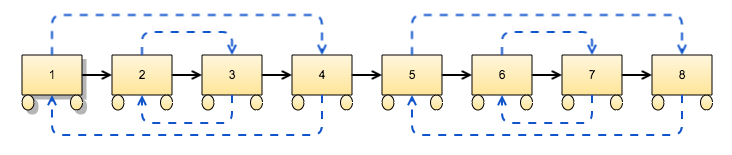
Let’s get moving then. We need to relocate passengers before the train starts!
What would we do in such a scenario?
First, get a EV or a segway.
Pick the 1st bogie passenger, take the EV to the nth bogie and put him there.
Pick the passenger in the nth bogie and get him to the first.
Now pick the passenger in the 2nd bogie and move all the way to (n-1)th bogie.
Repeat the above for all passengers, and
Reset the reversal schedule for every n passengers.
Diagrammatically, the below:
Great, let’s start hacking some code now.
Brute Force Approach
Move items one by one, revisiting every item
/* root refers to the root of the singly linked list
and 'n' the group size of the sub linked list */
/* variable used to traverse every node, we start with the root.*/
SNode node = root;
/* variable used to keep track of the node position
to identify pockets or sublists */
Integer nodeCount = 0;
/* variables used to performing swapping within a pocket of nodes */
Integer pocket = null;
Integer count = 0;
/* Until we reach the end of list */
while (null != node) {
// pick a pocket of nodes
if (nodeCount % n == 0) {
pocket = n;
}
if (pocket > 0) {
count = 1;
SNode newPos = node;
while (count % pocket != 0 && newPos.getNext() != null) {
newPos = newPos.getNext();
count++;
}
swap(node, newPos);
/* -2 because, 2 nodes are out of the equation
* one in front, and one in the end */
pocket = pocket - 2;
}
node = node.getNext();
nodeCount = nodeCount + 1;
}
The swap function, swaps the values of two nodes as below
Integer temp = node1.getData();
node1.setData(node2.getData());
node2.setData(temp);
The full code is available @ my tnut github page
For details refer tnut controller’s, “brute” api.
Feel free to fork/clone the same and run it on your local.
Refer t-nut repo for instructions to run.
Time for Retrospective
Kudos, we seem to have got a working solution.
Let see, if we our current strategy is taking us on the right path and if we can optimize.
As I had said earlier, retrospection is a critical phase of chewing on our solution.
Let’s be critical, shall we?
First, the solution seems to be work. Feel free to try out all cases on the swagger UI.
But look at the code above.
For every bogie passenger, we keep moving back and forth, and back and forth.
We keep traversing the same list, multiple times. Doesn’t seem effective.
Thank God, there is only one passenger per bogie. What would we do if there were more?? We would have to make more trips which is extremely inefficient
Wait a second, let’s pull a feather out of that idea. Why don’t we pick all “n” passengers in a subgroup at once and relocate them as a whole?
Let’s try that next up.
Step 4 - Take more bites
During our last retrospective, we realised that our logic wasn’t very efficient and there was room for improvisation.
Let’s adapt then.
This time, I’ll get a bigger EV and keep putting passengers from each bogie, within a subgroup, into my vehicle.
Once passengers from all “n” nodes in the subgroup have been accumulated, I’ll start from the last bogie and relocate the passengers in reverse order, i.e, the first bogie passenger in the last and so on.
Come let’s try hacking code for this approach
Step 5 - Swallow the next bite
Let’s devise a workable logic for the above strategy.
I’ve to pick “n” passengers in a sub group together, but I cannot start from the last bogie as I stated earlier. That’s because I cannot traverse in reverse direction in a singly linked list.
So I’ll start from the first bogie but place the passengers in reverse order.
This seems like a typical stack. I’ll add the passengers into the stack but pop them out in a LIFO manner as in a typical stack.
/* root refers to the root of the singly linked list
and 'n' the group size of the sub linked list */
/* variable used to identify the current pocket of nodes we are dealing with */
SNode currentRoot = root;
SNode node = root;
/* variable used to keep track of the node position to identify pockets */
Integer nodeCount = 0;
/* stack used to place nodes in appropriate positions */
Stack<Integer> stack = new Stack<>();
/* Until we reach the end of list */
while (null != node) {
// pick a subgroup
if (nodeCount % n == 0) {
relocate(stack, currentRoot, n);
currentRoot = node;
}
stack.push(node.getData());
node = node.getNext();
nodeCount = nodeCount + 1;
}
The relocate function would be a typical stack pop as below:
Integer count = 1;
while (count!=n) {
currentRoot.setData(stack.pop());
currentRoot = currentRoot.getNext();
count++;
}
Time for Retrospective
The solution looks pretty neat. But let’s critically review it once.
At even the best case, we need to traverse every node in the list twice.
Once, to pick the member from the bogie and again, to put the right member in place.
The time complexity is still O(n) though. The stack atleast made the code neat.
Guess we are getting to the end of this. Let’s carefully nibble the remnants.
The full code is available @ my tnut github page
For details refer tnut controller’s, “bruteStack” api.
Feel free to fork/clone the same and run it on your local.
Refer t-nut repo for instructions to run.
Step 6 - Optimize the final bites
Time to see if we’ve missed something out. Let’s check for some opening.
Some edge case, some NPE… something
Oh, the relocation function seems a little botched up.
It seems to be counting till the pocket size “n”, but the typical edge case we identified earlier would fail in this case.
We would get a index out of bounds exception. Using the counter thus, is not so catchy. Let’s try something cheesy.
while (!stack.empty()) {
currentRoot.setData(stack.pop());
currentRoot = currentRoot.getNext();
}
Alright, that should do. What else?
What about a empty input scenario? This should return an empty array and it seems to work.
What about a pocket size of 1 (n=1)? That should return the input array as is and that also seems to work as well.
Hey, there’s another observation.
The logic seems to empty the stack filled in one cycle, only in the subsequent cycle.
Observe how relocate is called, only after the stack is filled. But this means, the last set of ‘n’ passengers will never be put in place.
Bah!!! Why you ask? That’s because we would have reached the end of list. Let’s fix that.
We need to call relocate again after the while loop. That does it.
relocate(stack, currentRoot);
The full code is available @ my tnut github page
For details refer tnut controller’s, “bruteStack” api.
Feel free to fork/clone the same and run it on your local.
Refer t-nut repo for instructions to run.
Step 7 - Perpetual Optimization
We are almost done here, aren’t we?
But is that the best we could do though?
Let’s re-look at our last retrospect.
At the best case, we traverse every node twice.
That’s not nice, is it?
Not at all…
We can argue that the time complexity is still O(n) but time complexity is just one side of the story. It does give you the proportionality of time taken wrt to input size but does not shed light onto the rate of increase of time taken wrt to input size.
We’ll look at time complexity in detail in a later blog post but what I mean is traversing the list twice is any day worse than traversing it once. So there is room for improvement.
Really? Is there room for improvement? We did the best we could do there, didn’t we?

Well, I do not want to take the fun out of the moment. That’s all we live for.
We have cracked the T-Nut and we have done great.
All I’m saying is we can do better.
Bask in the glory, enjoy the success and when you are ready to move on and do better, hop over.
Cya here soon.
Gentle reminder
All the above tricks and solutions are available in my tnut github page
For details refer tnut controller
Feel free to fork/clone the same and run it on your local.
Refer t-nut repo for instructions to run.
The Genesis
How many of you are excited by etymology?
It’s always fun to know where things originate from, isn’t it?
More often than not, it will be via an expected source or scenario.
Let’s hear the anecdote from where this problem emerged.
It was tea time, a platform for imbecile discussions.
As we sat near the window, sipping hot tea and staring into the sunlight, Little B was deliberating over a domain change request, pertaining to a typical product shipment scenario.
In their E-Commerce world, once the product is approved for shipment, the process flow is as below
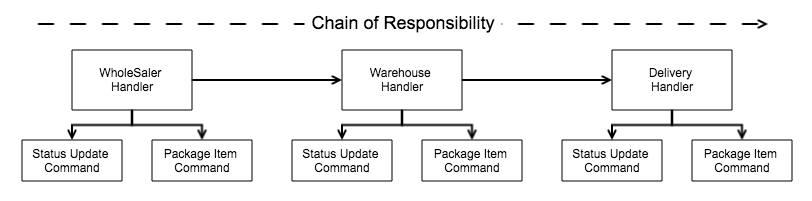
This was implemented as a chain of responsibility, with each shipment site representing a handler with two commands.
Updating the status, triggers a notification on the customer’s device.
Quite often, the handler packaging the item, irrecoverably failed after status update. This lead to a series of corrective status updates which could have been prevented had the status been updated only after a successful item packaging to begin with.
So, the execution of commands at each shipment site was decided to be reversed
That’s pretty trivial. Nothing to lost your mind over.
But little B was lost in thought, pondering about something…
Well, if you ever knew little B, things were more than what meets the eye with him.
He sat hands clasped, and looked into the distance, eyes transfixed into the unknown…
As if seeing something, we could not….
That’s when he contrived this hypothetical nut.
On slight improvisation of his given change request, he viewed the above chain as a singly linked list.
And boom… he concocted a challenge… to selectively reverse nodes on the linked list. Specifically reverse every “n” node sub groups in the big list where “n” is a variable input.
Interesting huh?
Life’s beautiful…